Nassim Nicholas Taleb1,2
1 Universa Investments, USA
2 Tandon School of Engineering, New York University, New York, USA
Correspondence to: Nassim Nicholas Taleb, email: nnt1@nyu.edu
11 June 2020
Link to the full opinion paper by Nassim N. Taleb, Yaneer Bar-Yam and Pasquale Cirillo (final version, from 3 August 2020): On single point forecasts for fat tailed variables
MAIN STATEMENT
- – Forecasting single variables in fat tailed domains is in violation of both common sense and probability theory.
- – Pandemics are extremely fat tailed.
- – Science is not about making single points predictions but understanding properties (which can sometimes be tested by single points).
- – Risk management is concerned with tail properties and distribution of extrema, not averages or survival functions.
- – Naive fortune cookie evidentiary methods fail to work under both risk management and fat tails as absence of evidence can play a large role in the properties.
COMMENTARY
Both forecasters and their critics are wrong: At the onset of the COVID-19 pandemic, many researcher groups and agencies produced single point “forecasts” for the pandemic — most relied on the compartmental SIR model, sometimes supplemented with cellular automata. The prevailing idea is that producing a numerical estimate is how science is done, and how science-informed decision-making ought to be done: bean counters producing precise numbers.
Well, no. That’s not how “science is done”, at least in this domain, and that’s not how informed decision-making ought to be done. Furthermore, subsequently, many criticized the predictions because these did not play out (no surprise there). This is also wrong. Both forecasters (who missed) and their critics were wrong — and the forecasters would have been wrong even if they got the prediction right.
Statistical attributes of pandemics: Using tools from extreme value theory (EVT), Cirillo and Taleb [1] determined that pandemics are patently fat tailed (with a tail exponent patently in the heaviest class1: α < 1 ) — a fact that was well known (and communicated by Benoit Mandelbrot) but not formally investigated. Pandemics do represent existential risk. The implication is that much of what takes place in the body of the distribution is just noise. One must not forecast, discuss, or theorize from noise. But it does not mean we can ignore the — very tractable — attributes as in fact they were shown to have remarkably stable extreme value properties.
Remark 1
Random variables with unstable (and uninformative) sample moments may still have stable tail properties centrally useful for inference and risk taking. a
a This is the central problem with the misunderstanding of The Black Swan: some events have stable and well known properties yet do not lend themselves to prediction.
Fortune cookie evidentiary methods: At about the same time Ioannidis (2020) [2] made statements to the effect that one should wait for “more evidence” before acting with respect to the pandemic, claiming that “we are making decisions without reliable data”.
Firstly, there seems to be a huge probabilistic confusion. We do not need more evidence under fat tailed distributions — it is there in the properties themselves (properties for which we have ample evidence) and these clearly represent risk that must be killed in the egg (when it is still cheap to do so). Secondly, unreliable data — or any source of uncertainty — should make us follow the most paranoid route. The entire idea of the author’s Incerto is that more uncertainty in a system makes precautionary decisions very easy to make (if I am uncertain about the skills of the pilot, I get off the plane).
More generally, evidence follows, does not precede, rare impactful events and waiting for the accident before putting the seat belt on, or evidence of fire before buying insurance would make the perpetrator exit the gene pool. As the Latin sayings: cineri nunc medicina datur (one does not give remedies to the dead) or post bellum auxilium ([one must not] send troups after the battle).
Remark 2: Fundamental Risk Asymmetry
For matters of survival, particularly when systemic, under such classes as multiplicative pandemics, we require “evidence of no harm” rather than “evidence of harm”.
MORE TECHNICAL COMMENTARY
LLN and Evidence: In order to leave the domain of ancient divination (or modern anecdote) and enter proper empirical science, forecasting must abide by both evidentiary and probabilistic rigor. Thus any forecasting activity requires the working of the law of large number (LLN), in other words, some convergence at a known rate so one can establish some significance given n observations. This is well known and established… except that many are not aware that, with the theory remaining exactly the same, the story changes under fat tails.
If one claims fitness or nonfitness of a forecasting ability based on a single observation n = 1, she or he would be deemed to be making an unscientific claim. For fat tailed variables that “n = 1″ error can be made with n = 106. In the case of pandemics, n = ∞ is still anecdotal.
Random variables in the power law class with tail exponent α ≤ 1 are, simply, not forecastable. They do not obey the LLN. But we can still understand their properties.
As a matter of fact, owing to preasymptotic properties, a heuristic is to consider variables with up to α ≤ 5/2 as not forecastable — the mean will be too unstable and requires way too much data for it to be possible to do so in reasonable time. It takes 1014 observations for a “Pareto 80/20” (the most commonly referred to probability distribution, that is with α ≈ 1.13) for the average thus obtained to emulate the significance of a Gaussian with only 30 observations.
Assuming significance with a low n in relation to the properties of the variable is an insult to everything we have learned since Bernoulli, or perhaps even Cardano.
Science is about understanding properties, not forecasting single outcomes: Figures 1 and 2 show the extent of the problem of forecasting under fat tails. Most of the information is away from the center of the distribution.
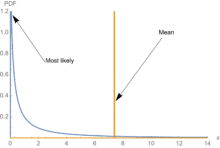
Fig. 1. A high-variance Lognormal distribution. 85% of observations fall below the mean. Half the observations fall below 13% of the mean (here 1). The lognormal has milder tails than the Pareto which has been shown to represent pandemics.
In some situations of fast-acting LLN, as in physics, properties can be revealed by single predictive experiments. But it is a fallacy to assume from that that single predictive experiments must be able to test any theory — though an n = 1 tail event with low conditional probability can falsify a theory.

Fig. 2. A Pareto distribution with a tail similar to that of the pandemics. Makes no sense to forecast a single point. The “mean” is so far away you almost never observe it. You need to forecast things other than the mean. And most of the density is where there is noise.
Sometimes, as has been shown in the International Journal of Forecasting by the author (just off the press, [3]), the forecaster may find a single variable that is forecastable, say the survival function which is uninformative for risk (or any practical purpose). In fact, tail survival functions have errors, for n observations of o(1/n), even when tail moments are not tractable, which is why many predict binary outcomes — as with the “superforecasters” masquerade. In fact the paper shows how the more intractable the higher moments of the variable, the more tractable the survival function. Metrics such as the Brier score are well adapted to binary survival functions, though not to the corresponding random variables. In finance and insurance, for instance, one never uses survival functions for risk management or hedging, only expected shortfalls — binary functions are reserved to (illegal) gambling. See paper for ample details.
Never cross a river that’s 4 feet deep on average: As we saw, risk management (or policy making) focuses on tail properties not the body of probability distributions. For instance, Holland has a policy to calibrate their dams not on average height of sea levels but on the properties of the maxima — all it takes is one mistake to cause a disaster.
Science is not about safety: Finally, science is a procedure to update knowledge; it can be wrong provided it produces interesting discussions that lead to more discoveries. But real life is not an experiment. If we used a p-value of 0.01 or other method of statistical comfort for airplane safety, no pilot would be alive. For matters that have systemic effects and/or entail survival, the asymmetry is even more pronounced.
REFERENCES
1. P. Cirillo and N. N. Taleb, “Tail risk of contagious diseases,” Nature Physics, vol. 16, pp. 606-613, 2020.
2. J. P. Ioannidis, “A fiasco in the making? as the coronavirus pandemic takes hold, we are making decisions without reliable data,” Stat News, 17 March 2020.
3. N. N. Taleb, “On the statistical differences between binary forecasts and real-world payoffs,” International Journal of Forecasting, available online, 2020.
1 Simple characterization of the power law class by the survival function: for X in the tails, P(X > x) = Kx-α, where K is a constant.

